以文本方式查看主题

-  胡老师的个人家教中心--15年专注1对1初中家教服务  (http://7742180.com/bbs/index.asp)
--  --+小文专区+--  (http://7742180.com/bbs/list.asp?boardid=7)
----  求证：两两相交而不过同一点的四条直线必在同一平面内．  (http://7742180.com/bbs/dispbbs.asp?boardid=7&id=979)
--  作者：小文
--  发布时间：2012/3/7 10:49:46
--  求证：两两相交而不过同一点的四条直线必在同一平面内．
求证：两两相交而不过同一点的四条直线必在同一平面内．
分析：
    四条直线两两相交且不共点，可能有两种：一是有三条直线共点；二是没有三条直线共点，故而证明要分两种情况．

              
此主题相关图片如下：
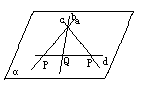
按此在新窗口浏览图片

（1）已知：d∩a＝P，d∩b＝Q．
           d∩c＝R，a、b、c相交于点O．
    求证：a、b、c、d共面．
    证明：∵d∩a＝P，
          ∴过d、a确定一个平面α（推论2）．
            同理过d、b和d、c各确定一个平面β、γ．
          ∵O∈a，O∈b，O∈c，
          ∴O∈α，O∈β，O∈γ．
          ∴平面α、β、γ都经过直线d和d外一点O．
          ∴α、β、γ重合．
          ∴a、b、c、d共面．
    注：本题的方法是“同一法”．

            
此主题相关图片如下：
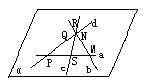
按此在新窗口浏览图片

（2）已知：d∩a＝P，d∩b＝Q，d∩c＝R，a∩b＝M，b∩c＝N，a∩c＝S，且无三线共点．
     求证：a、b、c、d共面
     证明：∵d∩a＝P，
           ∴d和a确定一个平面α（推论2）．
           ∵a∩b＝M，d∩b＝Q，
           ∴M∈α，Q∈α．
             MQα即bα.
             同理Cα
           ∴a、b、c、d四线共面．