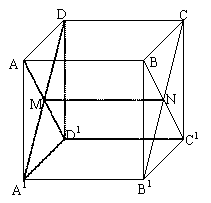
如图,在正方体ABCD—A′B′C′D′中,画出平面ABC′D′和平面A′B′CD的交线。
解:连接AD′和A′D交于M,连接BC′和B′C交于N。
∵M∈直线AD′,AD′ 平面ABC′D′,
平面ABC′D′,
∴M∈平面ABC′D′;
又M∈直线A′D,A′D  平面A′B′CD,
平面A′B′CD,
∴M∈平面A′B′CD。
所以点M是平面ABC′D′和平面A′B′CD的公共点。同理,点N也是平面ABC′D′和平面A′B′CD的公共点。连接MN,根据公理2,可知直线MN就是平面ABC′D′和平面A′B′CD的交线。
评注 确定两个平面的交线,关键在于确定两个平面的两个公共点,这两个公共点的连线就是这两个平面的交线。而确定两个平面的公共点,一般要在两个平面内分别找一条直线,且这两条直线相交。












 此主题相关图片如下:
此主题相关图片如下: